Spatiotemporal evolution of high power laser pulses in relativistic magnetized inhomogeneous plasmas
Physics of Plasma 22, 092310 (2015)
https://doi.org/10.1063/1.4930272
In this work, the spatiotemporal evolution of Gaussian laser pulse propagating through a plasma is investigated in the presence of an external axial magnetic field. The effect of the axial magnetic field on simultaneously relativistic self-focusing and self-compression of the laser pulse is studied for homogeneous and inhomogeneous plasmas.
Chirped Pulse Amplification (CPA) is a common method to amplify the laser pulse that uses dielectric gratings. These dielectrics cannot tolerate high intensities and perform below the 30 fs. Because of these limitations, a new method needs to be used to achieve higher intensities and shorter pulses. The plasma medium is proposed as an alternative to amplify laser pulses. With the advent of ultra-high intensity laser pulses, the relativistic self-compression (RSC) of laser pulses in the plasma is proposed as an amplification method. The high electric field associated with the propagation of high power laser pulses leads to a quiver motion of electrons on the order of the speed of light in a vacuum. This caused a significant increase in the mass of electrons and a consequent increase in the dielectric constant of the plasma, which leads to the dependence of the refractive index on the intensity. Therefore, the relativistic mass variation during the laser-plasma interaction is the main source of nonlinearity. The transverse gradient of the nonlinear refractive index is responsible for relativistic self-focusing (RSF), while the longitudinal gradient of the refractive index leads to the RSC. In the relativistic self-phase modulation (RSPM), the intensity dependence of the refractive index in the axial dimension produces the frequency chirp. Therefore, the leading edge of the pulse shifts to lower frequencies while the trailing edge shifts to higher frequencies. Since the plasma has the anomalous dispersion property, the higher frequencies (back of the pulse) move faster than, the lower frequencies (front of the pulse), and consequently, the pulse would be compressed while it propagates through the plasma.
In this regard, we aimed to investigate both effects of the external axial magnetic field and plasma inhomogeneity on simultaneously self-focusing and self-compression of a laser pulse through the plasma.
Consider a collisionless magnetized plasma with the static magnetic field \(B_0z\) and the density ramp-up profile which is presented by the following equation:
\begin{equation}\label{equ1}
n(z)=n_0(1+d \times z)
\end{equation}
where n0 is the plasma density in z=0, and d is an adjustable constant which represents the slope of the ramp.
The dielectric function of plasma can be expanded as a series in r2 and s2 as follows:
\begin{equation}\label{equ2}
\varepsilon(r,z,\tau)=\varepsilon_0(z)-\frac{r^2}{r_0^2}\varepsilon_r-\frac{\tau^2}{\tau_0^2}\varepsilon_\tau,
\end{equation}
Where \(\varepsilon_r=-\frac{\partial \varepsilon}{\partial |A|^2}\frac{\partial |A|^2}{\partial r^2}r_0^2\), \(\varepsilon_\tau=-\frac{\partial \varepsilon}{\partial |A|^2}\frac{\partial |A|^2}{\partial \tau^2}\tau_0^2\), \(\tau=t-z/v_g\) is the retarded time and \(v_g=d\omega/dk=c^2k/\omega\) is the group velocity which can be obtained from the plasma dispersion relation.
The solutions can be anticipated in the form
\begin{equation}\label{11}
A_0^2(r,z^\prime,\tau)=\frac{A_{00}^2}{f^2g}exp\left(\frac{-r^2}{r_0^2f^2}\right)exp\left(\frac{-\tau^2}{\tau_0^2g^2}\right),
\end{equation}
where \(f=f(z)\) and \(g=g(z)\) represent the dimensionless beam width and pulse length parameters respectively.
Using the variables \(\xi=z^\prime\omega/c\), \(\rho=r_0\omega/c\) and \(\tau_p=\tau_0\omega/c\) the coupled equations of self-focusing and self-compression of the laser pulse can be obtained.
\begin{equation}\label{13}
\varepsilon_0\frac{\partial^2f}{\partial \xi^2}=\frac{1}{\rho^4
f^3}-\frac{f\varepsilon_r}{\rho^2}-\frac{1}{2}\frac{\partial\varepsilon_0}{\partial\xi}\frac{\partial
f}{\partial\xi},
\end{equation}
\begin{equation}\label{14}
\varepsilon_0\frac{\partial^2g}{\partial
\xi^2}=\frac{\beta}{\tau_p^4 g^3}-\frac{\beta
g\varepsilon_\tau}{\tau_p^2}-\frac{1}{2}\frac{\partial\varepsilon_0}{\partial\xi}\frac{\partial
g}{\partial\xi},
\end{equation}
where \(\beta=(1-\varepsilon_0)/(c^2\varepsilon_0)\).
These equations determine the spatiotemporal evolution of laser pulse as it propagates through the magnetized plasma with the density ramp-up.
In order to investigate the spatiotemporal evolution of laser pulse in the magnetized plasma, the coupled equations 4 and 5 must be solved numerically. Equation 4 is known as the self-focusing equation and determines the focusing/defocusing of the laser beam. The first term on the right-hand side of the mentioned equation represents the diffraction while the second term is responsible for relativistic self-focusing. The longitudinal self-compression of a laser pulse can be explained by equation 5. The first term on the right-hand side represents the dispersion broadening, and the second term explains compression of the laser pulse due to the relativistic effect. In both equations, the focusing and compression processes can occur when the magnitude of the second term becomes larger than the first one. The third term on the right-hand side of equations 4 and 5 is due to the plasma inhomogeneity. The coupled equations 4 and 5 can be solved numerically using the fourth-order Runge-Kutta technique with the boundary conditions \(f=g=1\) and \(\partial f/\partial\xi=\partial g/\partial\xi=0\) in \(\xi=0\).
Other laser's and plasma's parameters are as follows:
| Parameter | Value |
| Wavelength (λ) | 800 nm |
| Laser spot size (r0) | 20 μm |
| Laser pulse length (τ0) | 50 fs |
| Initial plasma density (n0) | 1.5×1018cm-3≈10-3ncr |
| Initial laser intensity (I0) | 5×1017W/cm-2 |
| Initial normalized laser (\(A_{00}^2\)) |
0.2 |
| Ramp parameter (d) | 0.4 |
For the first step, let us investigate the effect of the static magnetic field on the spatiotemporal evolution of the laser pulse. In this regard, by solving the coupled equations 4 and 5, the variation of beam width (\(f\)) and pulse length (\(g\)) parameters are plotted with a normalized distance of propagation in Fig. 1(a) for different values of \(\omega_c\) in initially homogeneous plasma with no density ramp. At first glance, one can see that in all cases (with different \(\omega_c\)), the relativistic self-compression assists the self-focusing mechanism. The relativistic nonlinearity results in compression of the pulse in a longitudinal direction. Therefore, the pulse intensity is increasing due to the compression mechanism. On the other hand, it is known that the strength of relativistic self-focusing becomes improved when the laser intensity increases16. As a result, by compressing the pulse, the self-focusing becomes stronger, and the maximum spot size of the laser decreases as the laser pulse penetrates the plasma. It is also clear from Fig. 1 that by increasing the magnetic field, the self-focusing and self-compression mechanisms are improved. The pulse becomes compressed in a shorter distance of propagation. As a result, the maximum spot size of the laser pulse in transverse direction decreases as the strength of the magnetic field rises. In Fig. 1(b) one can see the compression of laser pulse after passing about \(z=1.8 cm\) with different initial \(\omega_c\). As it is seen from this figure, the higher magnetic field results in better pulse compression. The high electric field of the laser induces a large oscillatory velocity on electrons, raising their relativistic mass and lowering the plasma frequency. The cyclotron resonance enhances this effect. Therefore, as the magnetic field rises, the nonlinear effects become more pronounced. Thus the relativistic focusing and compression are enhanced by increasing the magnetic field.
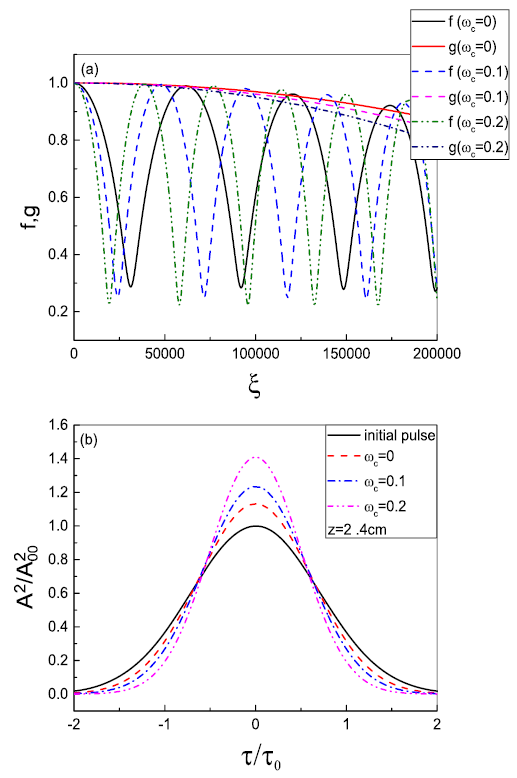
FIG. 1 The effect of external axial magnetic field on the (a) variation of \(f\) and \(g\) parameters with the normalized distance of propagation and (b)
compression of laser pulse after passing through the plasma \(z=2.4 cm\)
For a better understanding, in Fig. 2, the normalized effective plasma density \(n_{eff} /n_0\) is sketched versus the normalized distance of propagation. In this figure, it is seen that in the absence of the magnetic field, the gamma factor decreases the effective plasma density from its initial value of \(n_0\). In the presence of an external magnetic field, it is seen that the initial effective plasma density at \(z=0\) is increased and the higher cyclotron frequency results in higher effective plasma density. On the other hand, it was mentioned that the second term on the right-hand side of Equation 4 is responsible for self-focusing. by increasing the effective plasma density, the second term on the right hand of Equation 5 also increases. As was mentioned, this term is responsible for the self-compression phenomenon. Therefore, the strength of the self-compression mechanism also would be increased by increasing the value of cyclotron frequency. So it is concluded that the self-focusing and self-compression phenomena are enhanced as the external magnetic field goes up. From Fig. 2, it is also indicated that the effective plasma density oscillates due to the relativistic gamma factor oscillation. In fact, the \(f\) parameter determines the spot size of a laser and consequently the normalized intensity of the laser while it propagates in the plasma. On the other hand, normalized intensity determines the relativistic gamma factor. Therefore, as it is predictable, the oscillation frequency of the effective plasma density is in accordance with those oscillation frequencies of f parameter in Fig. 1(a) for each case. It is also interesting to mention that as the pulse propagates in the plasma, the maximum value of effective plasma density (peaks of the curves in Fig. 2) decreases due to decreasing the maximum spot size of a laser beam through propagation which was mentioned above in the explanation of Fig. 1.
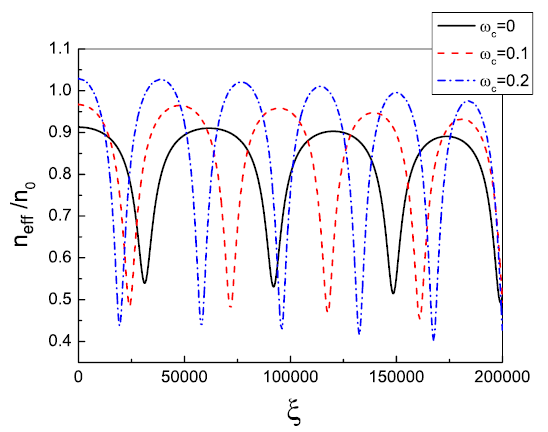
FIG. 2. The variation of normalized effective plasma density with a normalized the distance of propagation for different values of cyclotron frequency.
In Fig. 3(a), the f and g parameters are sketched with the normalized distance of propagation in a magnetized plasma with the density ramp-up with \(d=0.4\). The other parameters are the same as those in Fig. 1. Fig. 3(b) also indicates the pulse compression after passing about \(z=2.4 cm\) through the mentioned plasma. These diagrams show that both self-focusing and self-compression phenomena are more strengthened by using the plasma with the density ramp-up. Fig. 3(a) also shows that, by using the ramp structure, the maximum spot size of the laser pulse in the transverse direction is more decreased (in comparison with magnetized homogeneous plasma) because the relativistic mass effect will be much more pronounced in the region of increasing plasma density. In other words, as the initial plasma density is an increasing function of the propagation distance, the plasma dielectric constant decreases rapidly as the pulse penetrates deeper and deeper into the plasma. Therefore, one can conclude that, in addition to using the static axial magnetic field for improving the self-focusing and self-compression mechanisms, the ramp-up structure can be used to facilitate these phenomena.
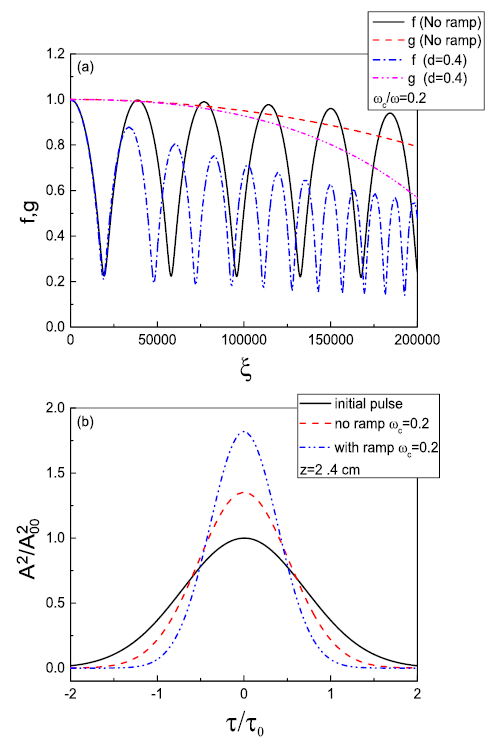
FIG. 4. The variation of normalized effective plasma density with
normalized the distance of propagation for different values of the ramp slope.
Figure 4 represents the effective plasma density versus normalized distance of propagation related to Fig. 3(a). In this figure, it is seen that, in the ramp-up case, first as the pulse propagates in plasma, the effective plasma density increases due to increasing the \(n(z)\) via ramp structure as it defines in Eq. (1). But as the pulse penetrates deeper into the plasma, the maximum effective plasma density starts to decrease since the relativistic gamma factor increases vastly due to the self-compression mechanism. Moreover, in this figure, also it is clear that the oscillation frequency of the effective plasma density is in accordance with those oscillation frequencies of f parameter in Fig. 3(a) for each case.

FIG. 5. The spatiotemporal evolution of laser pulses in (b) homogeneous unmagnetized plasma, (c) homogeneous magnetized plasma, (d) magnetized ramp plasma with \(d=0.4\), and (f) magnetized ramp plasma with \(d=50\) after passing about \(n\). Part (a) refers to the initial laser pulse.
Fig. 5 is generally referred to the spatiotemporal profile of the laser field intensity \(I=I_0\) by considering the relativistic nonlinearity at positions in which the beam has its maximum spot size (peaks of the self-focusing diagram in Figs. 1(a) and 3(a)). Figure 5(a) is related to the initial laser pulse before the propagation in the plasma. Figures 5(b), 5(c), 5(d), and 5(e) refer to the laser pulse self-focusing and self-compression in a homogeneous unmagnetized plasma, homogeneous magnetized plasma, magnetized ramp plasma with \(d=0.4\), and magnetized ramp plasma with \(d=50\), respectively. All the other laser and plasma parameters are set to be the same as those in Figs. 1 and 3. By comparing all the parts of Fig. 5, one can conclude that the highest intensity via self-compression and self-focusing can be achieved by using magnetized plasma with the ramp density profile. It is also evident that the higher ramp slopes result in stronger focusing and compression mechanisms. As it was mentioned above, the strength of focusing and compression mechanisms increases as the effective plasma density goes up (see Eqs. (13) and (14)). Therefore, it is predictable that these mechanisms must be more significant in higher plasma densities, especially in near-critical plasmas.
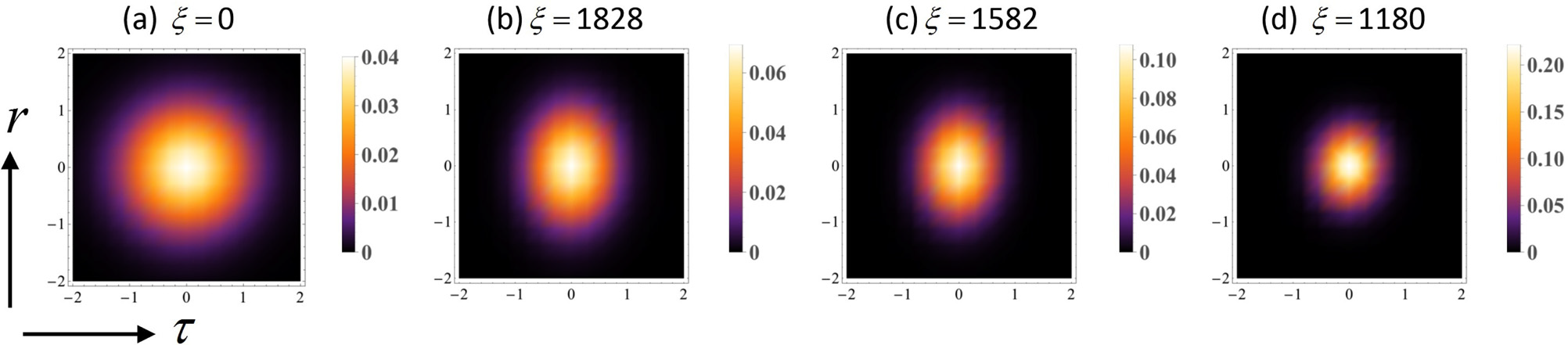
FIG. 6. The spatiotemporal evolution of a laser pulse in (b) homogeneous plasma, (c) homogeneous magnetized plasma, and (d) magnetized ramp plasma after propagation about n in near-critical plasma. Part (a) refers to the initial laser pulse.
In Fig. 6, the spatiotemporal profile of the laser field intensity \(I /I_0\) is sketched by considering the relativistic nonlinearity in near-critical density through the (b) homogeneous plasma, (c) homogeneous magnetized plasma, and (d) magnetized ramp plasma. In the homogeneous plasma, the plasma density is set as \(n_0=0.3n_{cr}\), and in the ramp case, the plasma density is set in a narrow window of plasma density values from \(0.3n_{cr}\) to slightly below \(n_{cr}\) with the ramp parameter \(d=50\), where \(n_{cr}=m{\omega}^2 /4\pi{e}^2\) is the critical density for the laser pulse with the frequency \(\omega=2 \pi c / \lambda\). By comparing Fig. 6(d) with Fig. 5(e) with the same ramp parameter \(d\), it is evident that the compression length decreases near-critical plasmas. So one can conclude that the relativistic compression process has its strongest strength near-critical plasmas where the relativistic effects are of real importance. Moreover, Fig. 6 shows that in near-critical plasma also the strongest focusing and compression can be achieved by using the magnetized plasma with the density ramp-up. Therefore, the gamma factor can be reached to higher values due to the best compression and focusing on magnetized ramp plasma. Thus, the laser light can propagate deeper into the overdense plasma due to higher values of relativistic gamma factor in magnetized ramp plasma which can be applicable in some applications such as Inertial Confinement Fusion (ICF). It is also interesting to mention that, by increasing the relativistic gamma factor, the critical surface transfers to a new position where the plasma density is about \(n=\gamma n_{cr}(1-\omega_c /\gamma \omega)\), which can be used in plasma optical shuttering design and fabrication.
In the end, we have investigated the spatiotemporal evolution of a Gaussian laser pulse in a relativistic magnetized plasma. Using the paraxial approximation approach, we have derived two coupled equations for the dimensionless pulse length (in the longitudinal direction) and beam width (in transverse direction) parameters whose evolution determines the dynamics of the pulse in space and time. In our results, first, we have studied the effect of the magnetic field strength on the combined self-focusing and self-compression phenomena and showed that both mentioned mechanisms are improved by increasing the magnetic field strength. Next, the effect of the linear ramp density profile is investigated in relativistic magnetized plasma and indicated that the laser focuses and compresses more during propagation in a magnetized plasma with the ramp density profile. In the last, we also have sketched diagrams showing spatiotemporal evolution of a laser pulse in the homogeneous unmagnetized, homogeneous magnetized, and inhomogeneous magnetized plasmas in both underdense and near-critical plasmas and indicated that in both cases the best focusing and compression could be reached in the presence of both magnetic field and ramp structure. Moreover, it is shown that the relativistic compression process has its strongest strength, near-critical plasmas. These results may be applicable in the context of plasma-based accelerators in which the self-guided propagation of laser pulses over a long distance is required along with the higher laser intensities. The results are also especially significant in plasma lens design and fabrication to make high intensity, high contrast laser pulses in experimental scientific investigations.