5th Iranian conference on engineering and physics of plasma

Pulse shape effect on backward Raman amplification of laser pulse propagation through a plasma

The 5th Iranian conference on engineering and physics of Plasma, Tehran, Iran

This article has been extracted from my thesis.

In this article, the pulse shape effect on amplification and self-compression of a laser pulse propagating through a Plasma has been investigated. For obtaining the largest output intensity, a set of coupled equations due to three-wave interaction in Raman scattering were solved. Effect of different laser pulse profiles such as Gaussian, super-Gaussian, Flattop and triangle on pulse amplification and responding to group velocity dispersion was analyzed. Results show that super-Gaussian profile due to aggregation of energy has the most considerable value of amplification. Also, the triangle profile has a better response to group velocity dispersion effect.

Chirped pulse amplification (CPA) is the most popular amplification method, which uses dielectric gratings. These dielectric gratings cannot tolerate hight intensities that cause limitation of output power. In order to overcome this limitation, other methods are being proposed. Plasma is a pre-broken down medium, which can barrel high intensities. Raman backscattering amplification (BRA) is known as an alternative. In this method, two counter-propagating laser pulses with a slight difference in frequencies \((\omega_p>\omega_s)\) collide with each other in a Plasma. Due to this, a Langmuir wave is excited that reflects the pump pulse. The energy of pump pulse is transformed into the seed pulse with the mediating of Plasma that amplifies it. In order to the BRA, the resonance condition needs to be satisfied:

\begin{equation}
\omega_p=\omega_s + \omega_l
\end{equation}

\(\omega_p\),\(\omega_s\), and \(\omega_l\) are pump pulse, seed pulse, and Langmuir frequency, respectively.

In order to achieve the highest output intensity, a one-dimensional model may be adequate. Amplification of seed pulse by consumption of the pump pulse will be solved by one-dimensional equations for the resonant 3-wave interaction. The lowest order of nonlinearity is given.

\begin{equation}\label{equ2}
\frac{\partial p}{\partial t}+c_p\frac{\partial p}{\partial z}=Cls, \frac{\partial l}{\partial t}=-Cps^*
\end{equation}
\begin{equation}\label{equ3}
\frac{\partial s}{\partial t}-c_s\frac{\partial s}{\partial z}=-Cpl^*+iN|s|^2s-id\frac{\partial^2 s}{\partial t^2}
\end{equation}

Here \(p\), \(s\) and \(l\) are envelopes of pump pulse, counter propagating pulse and resonant Langmuire wave, respectively; \(c_p\) and \(c_s\) are group velocities of pump pulse and counter propagating pulse. \(C\) is 3-wave coupling constant, \(N\) is coefficient of nonlinear frequency shift due to the relativistic electron nonlinearity and \(d\) is group velocity dispersion coefficient.

In a cold plasma, the Langmuir frequency is approximately equal to the plasma frequency (\(\omega_l\approx\omega_P\)).

To solve the equations numerically, we need to introduce two new dimensionless Variables. it is helpful to change \(z\) and \(t\) to dimensionless variables: \(\zeta\), measures the distance (or delay time) from the original seed front, \(\tau\) measures the elapsed amplification time (or the distance traversed by the original seed front). Where can be written as:

\begin{equation}\label{equ10}
\tau=(1+\frac{c_p}{c_s})^{1/3}N^{1/3}C^{2/3}_3p^{4/3}\frac{L-z}{c_s}
\end{equation}
\begin{equation}\label{equ11}
\zeta=(1+\frac{c_p}{c_s})^{-1/3}N^{-1/3}C^{4/3}_3p^{2/3}(t-\frac{L-z}{c_b})
\end{equation}

Where \(L\) is plasma width, \(t\) is process time. Amplified pulse injects into plasma at \(t=0\) and \(z=L\), the pump pulse arrived the end of plasma and the two pulses interact each other until amplified pulse leaves the plasma, and process will finish. Once the seed pulse have exited the plasma, the process will finish.

Having introduced new variables, new envelopes for pulses are defined.

\begin{equation}\label{equ12}
p=p_0p'
\end{equation}
\begin{equation}\label{equ13}
l=-p_0(1+\frac{c_p}{c_s})^{1/2}l'
\end{equation}
\begin{equation}\label{equ14}
s=(\frac{Cp^2_0}{N})^{1/3}(1+\frac{c_p}{c_s})^{1/6}s'
\end{equation}

By applying these new envelopes and dimensionless variables to coupled equations, these equations have found new form. By neglecting slow time derivative of pump amplitude compared to fast time derivative of the pump amplitude \((\frac{\partial p}{\partial \zeta}>>\frac{\partial p}{\partial \tau})\), one of the derivative term is removed. One obtains the following universal equations containing just one parameter \(D\):

\begin{equation}\label{equ15}
\frac{\partial p'}{\partial \zeta}=-s'l'
\end{equation}
\begin{equation}\label{equ16}
\frac{\partial l'}{\partial \zeta}=p's'^*
\end{equation}
\begin{equation}\label{equ17}
\frac{\partial s'}{\partial \tau}=p'l'^*-iD\frac{\partial^2 s'}{\partial \tau^2}+i|s'|^2s'
\end{equation}
\begin{equation}\label{equ18}
D=\frac{(k_p+k_s)c^2\omega_sc'_s}{4\omega_P\omega_p(c_p+c_s)}
\end{equation}

Equations \ref{equ15}-\ref{equ17} will be solved for initial constant sharp front pump pulse \(p'(\zeta,\tau=0)=1\) and zero Langmuir wave \(l'(\zeta=0,\tau=0)=0\).

For input seed pulse, we have used \(4\) different longitudinal laser profiles, that these profiles have the same energy but the maximum value of intensity are different.

Gaussian seed pulse:

\begin{equation}\label{equ19}
s'(\zeta,\tau=0)=0.028\times exp[-(\zeta-10)^2]
\end{equation}

Super-gaussian seed pulse:

\begin{equation}\label{equ20}
s'(\zeta,\tau=0)=0.026\times exp[-(\zeta-10)^{10}]
\end{equation}

Flattop seed pulse:

\begin{equation}\label{equ21}
s'(\zeta,\tau=0)=0.0024815
\end{equation}

Triangle seed pulse:

\begin{equation}\label{equ22}
s'(\zeta,\tau=0)=\left\{
\begin{array}{rl}
\zeta \times tan{0.000496299} & \zeta < 10\\
(20-\zeta) \times cot({\frac{\pi}{2}-0.000496299}) & \zeta \ge 10
\end{array} \right.
\end{equation}

Equations \ref{equ15}-\ref{equ17} will be solved by seed profiles \ref{equ19}-\ref{equ22}.

First, consider extremely under-critical plasmas where the group velocity dispersion can be neglected, so that the approximation \(D=0\) is good enough. So these equations can be solved by Euler method, and we observe saturation due to the REN regime.

The gaussian pulse has been amplified almost as same as super-gaussian pulse, but the flattop and triangle profiles have been amplified lesser at the first spike. At the second spike, there is a significant difference between the first couple and second couple amplified amplitude of pulses, even second couples of pulses don't have the third spike and without having the third spike leave the Plasma.

In the contract of first and second spikes, the amplified amplitude of gaussian and super gaussian profiles is getting attention, and super gaussian profile have been amplified more than other profiles.

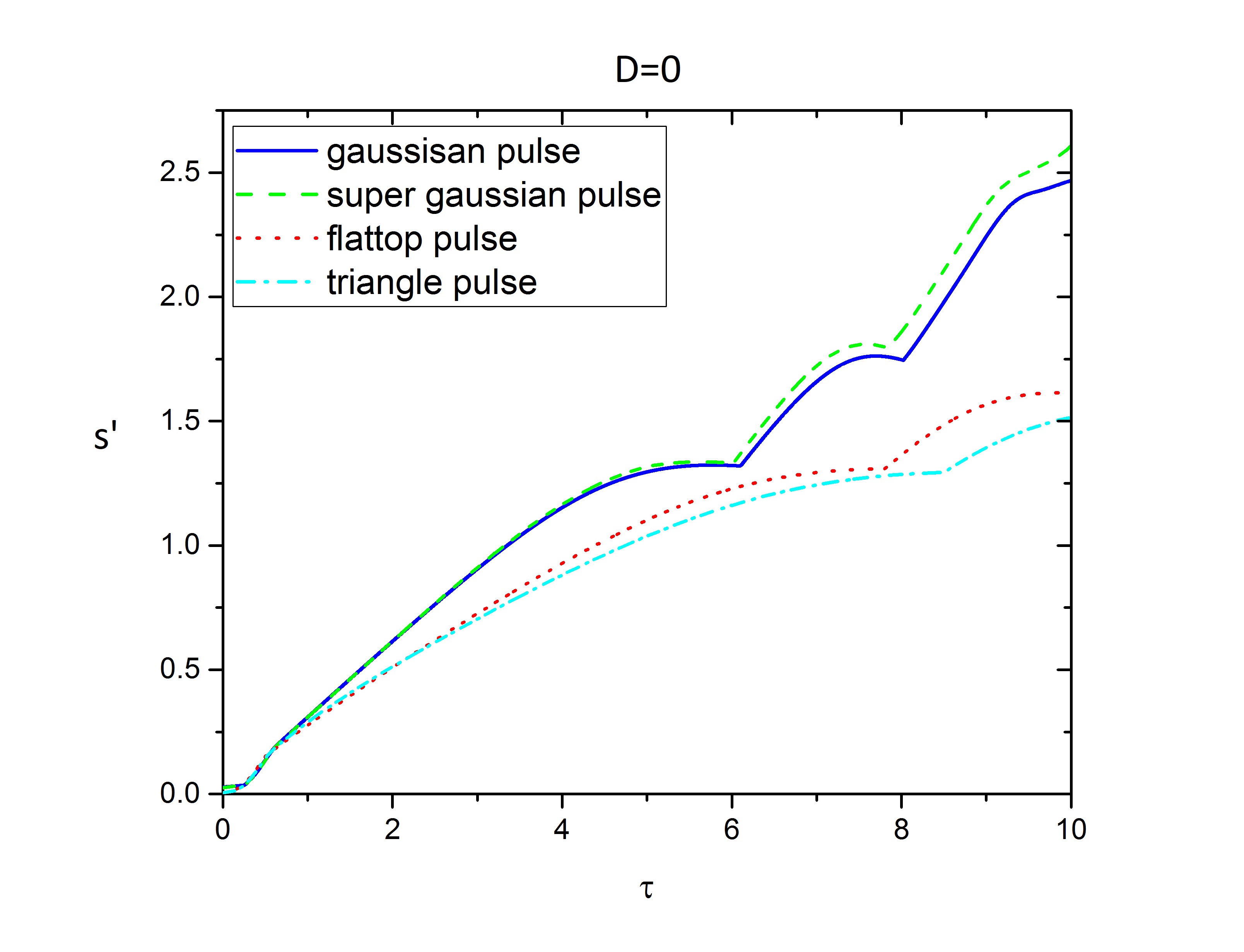
FIG. 1 maxim amplified amplitude of seed pulse during process time \(\tau\)

For less extreme, though still strongly under-critical plasmas, the group velocity dispersion can become important in the REN regime. The \(D=0.01\) can be a good approximation to solve \ref{equ15}-\ref{equ17} by the seed pulse profiles.

FIG. 2 indicates how group velocity dispersion affects the amplification of pulses, and the amplified value of profiles has been decreased. The considerable difference value of the amplified amplitude between two pair of profiles has been dropped, and the value of amplified profiles came close. There has almost the same amplified amplitude.

The main point is the flattop and triangle profiles resist against of group velocity dispersion more than Gaussian and super-Gaussian profiles. Their response is better, that makes them the right choice for dispersive media. Along with it, the third spike is growing weakly.

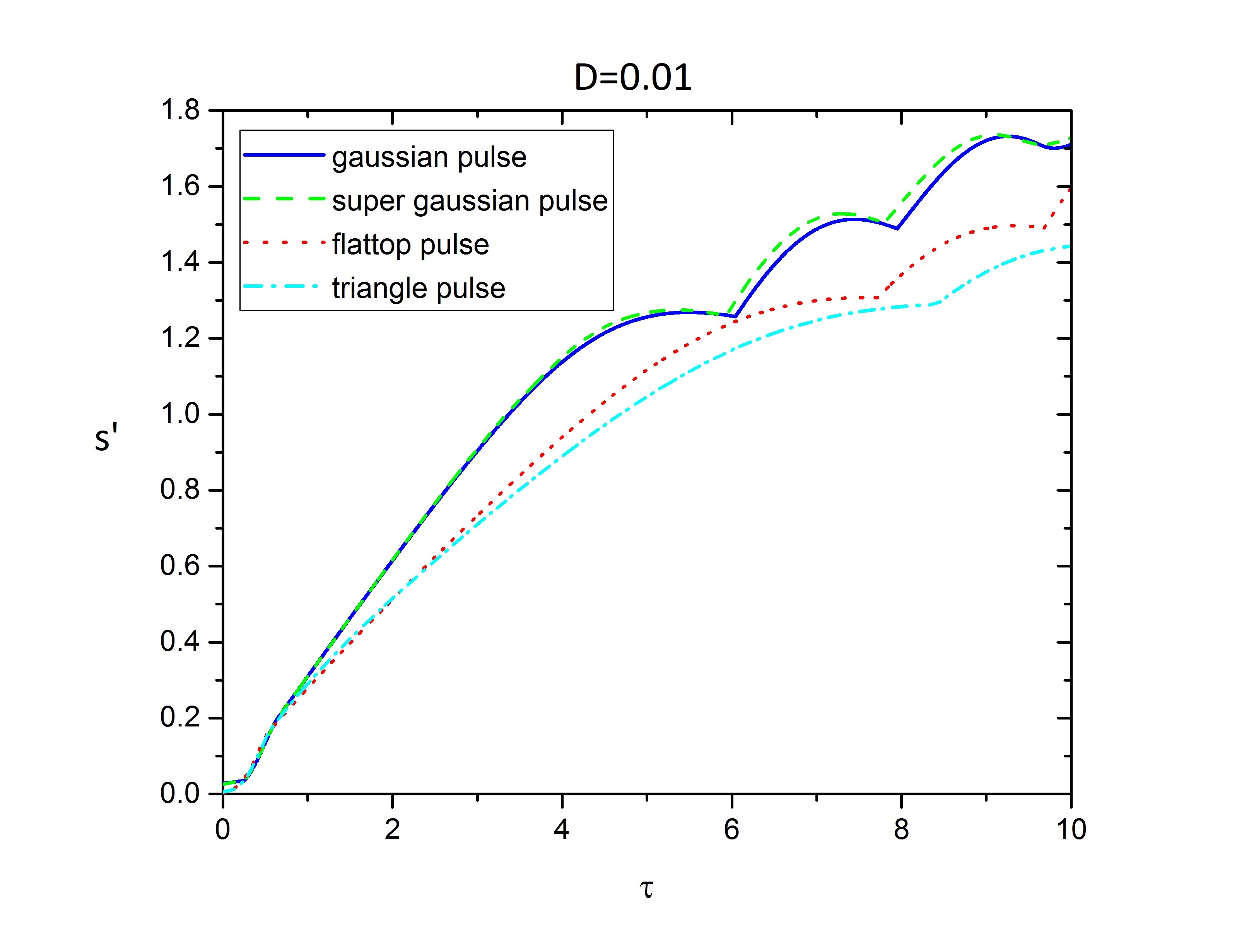
FIG. 2 maxim amplified amplitude of seed pulse during process time \(\tau\)

The effect of group velocity dispersion on the Gaussian and super-Gaussian profile is noticeable; on the other hand, group velocity dispersion doesn't have a significant impact on Flattop and triangle profiles. It shows that a second couple of profiles are a better option for dispersive media; they can resist against of group velocity dispersion.

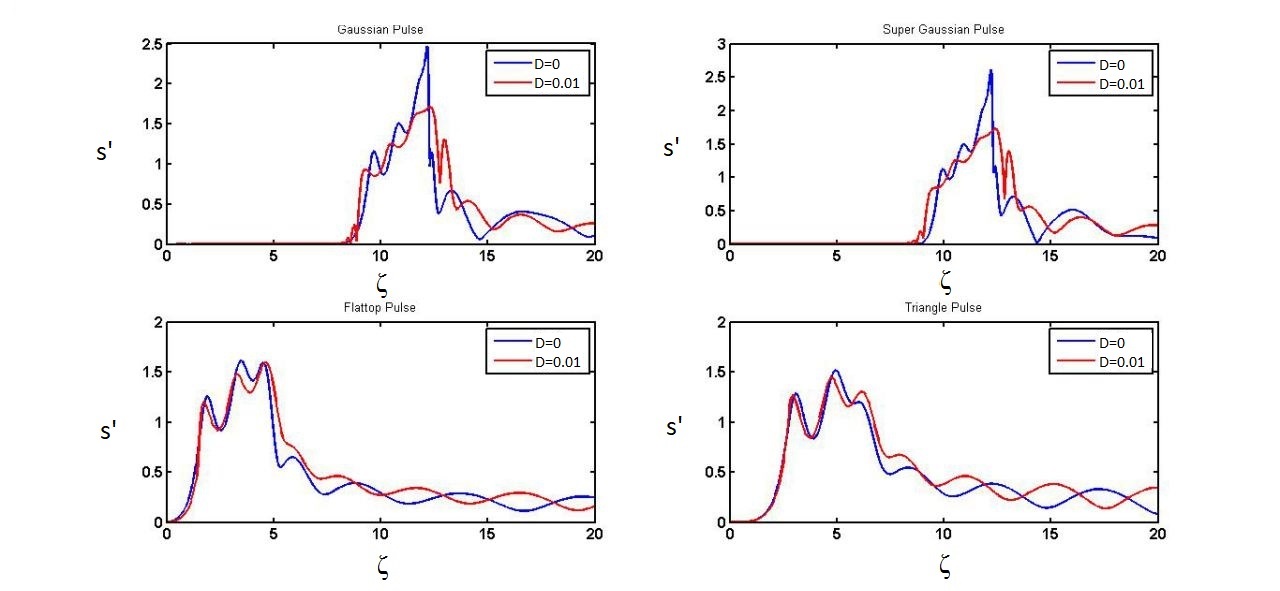
FIG. 3 comparison between final shape of amplified profiles

In summary, BRA is a novel method to amplify the laser pulses. The higher value of amplification, along with simultaneity of amplification and compression of pulses, make BRA an effective option to amplify the laser pulses.

Among the various longitudinal laser profiles, the super-Gaussian profile will be amplified more than other profiles because of the wider peak of amplitude. This profile has been amplified almost as much as Gaussian profile, but being narrow is a plus for that.

Although, in dispersive media Flattop and triangle profiles are more suitable option than others. They will be affected lesser than other profiles, and their response to group velocity dispersion makes them noteworthy.